nLab flop transition
Context
Geometry
higher geometry / derived geometry
Ingredients
Concepts
-
geometric little (∞,1)-toposes
-
geometric big (∞,1)-toposes
Constructions
Examples
-
derived smooth geometry
Theorems
String theory
Ingredients
Critical string models
Extended objects
Topological strings
Backgrounds
Phenomenology
Contents
Idea
The flop transition is a continuous path in a space of noncommutative 2-geometries that starts at an ordinary complex 3-dimensional Calabi-Yau space, then passes through a point that does not correspond to an ordinary geometry (the Gepner point) and emerges afterwards again as an ordinary CY-geometry – but now with different topology.
This was found and discussed in the context of string theory but the phenomenon is a general abstract one in the theory of 2d SCFTs regarded as generalized geometries – as described at 2-spectral triple.
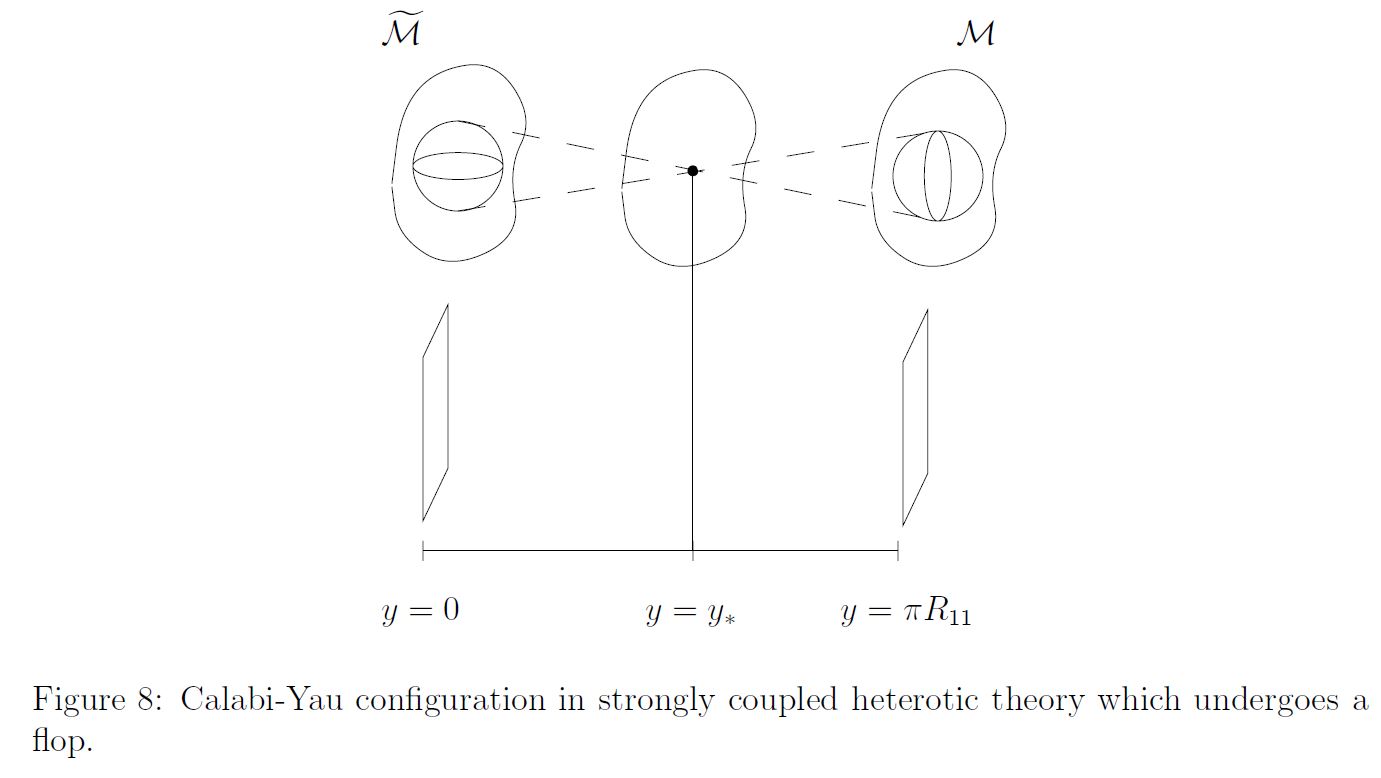
graphics grabbed from Greene 00
Related concepts
References
A survey is in
- Brian Greene, String Theory on Calabi-Yau Manifolds (arXiv:hep-th/9702155)
A rough and brief survey of the flop transition and related phenomena with many pointers to original literature is also given in
- Brian Greene, Aspects of collapsing cocycles, in Proceedings of Strings 2000, WorldScientific 2001 (pdf, doi:10.1142/4599)
See also
On the quantum volume? of vanishing cycles in the flop transition:
-
Brian Greene, Yakov Kanter, Small Volumes in Compactified String Theory, Nucl.Phys.B497:127-145,1997 (arXiv:hep-th/9612181)
-
Brian Greene, Calin Lazaroiu, Collapsing D-Branes in Calabi-Yau Moduli Space: I, Nucl.Phys. B604 (2001) 181-255 (arXiv:hep-th/0001025)
-
Calin Lazaroiu, Collapsing D-branes in one-parameter models and small/large radius duality, Nucl.Phys. B605 (2001) 159-191 (arXiv:hep-th/0002004)
-
Mark Raugas, D-Branes and Vanishing Cycles in Higher Dimensions (arXiv:hep-th/0102133)
Last revised on January 12, 2019 at 18:01:57. See the history of this page for a list of all contributions to it.